很久以前,相信很多人都在DirectX SDK的Picking程序示例中看到过一个叫做Pick.cpp的文件,其中有一个非常重要的函数——解决射线和三角形相交问题的函数,后期被很多3D项目使用,用在模型拾取功能上,成为调用最频繁的函数之一。下面就详细分析一下其中的计算公式。
(下文中粗体代表向量)
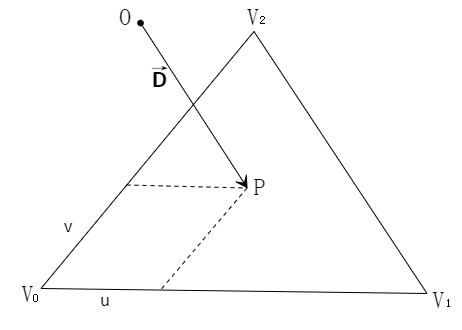
射线通常由起点和方向两部分数据组成,射线上的某个点表示为Pray = O + Dt。
设射线和三角面的交点为P,那么P = O + Dt = u(V1 - V0) + v(V2 - V0) + V0。
∴ u(V1 - V0) + v(V2 - V0) - Dt = O - V0。
设 E1 = V1 - V0,E2 = V2 - V0,T = O - V0。
可得 uE1 + vE2 - Dt = T。
再设 E1(xE1, yE1, zE1),E2(xE2, yE2, zE2),D(xD, yD, zD),T(xT, yT, zT)。
那么联立做方程组:
\[\begin{cases} x_{E1}u + x_{E2}v - x_D{t} = x_T\\ y_{E1}u + y_{E2}v - y_D{t} = y_T\\ z_{E1}u + z_{E2}v - z_D{t} = z_T\\ \end{cases}\]根据克莱姆法则得
\[u = \frac{D_1}{D}\] \[v = \frac{D_2}{D}\] \[t = \frac{D_3}{D}\]即
\[D = \begin{vmatrix} x_{E1} & x_{E2} & -x_D \\ y_{E1} & y_{E2} & -y_D \\ z_{E1} & z_{E2} & -z_D \\ \end{vmatrix} = \begin{vmatrix} \bf{E_1} & \bf{E_2} & -\bf{D}\\ \end{vmatrix}\] \[D_1 = \begin{vmatrix} x_T & x_{E2} & -x_D \\ y_T & y_{E2} & -y_D \\ z_T & z_{E2} & -z_D \\ \end{vmatrix} = \begin{vmatrix} \bf{T} & \bf{E_2} & -\bf{D}\\ \end{vmatrix}\] \[D_2 = \begin{vmatrix} x_{E1} & x_T & -x_D \\ y_{E1} & y_T & -y_D \\ z_{E1} & z_T & -z_D \\ \end{vmatrix} = \begin{vmatrix} \bf{E_1} & \bf{T} & -\bf{D}\\ \end{vmatrix}\] \[D_3 = \begin{vmatrix} x_{E1} & x_{E2} & x_T \\ y_{E1} & y_{E2} & y_T \\ z_{E1} & z_{E2} & z_T \\ \end{vmatrix} = \begin{vmatrix} \bf{E_1} & \bf{E_2} & \bf{T}\\ \end{vmatrix}\]又根据混合积公式\(\begin{vmatrix} \bf{A} & \bf{B} & \bf{C}\\ \end{vmatrix}\) = A × B · C = -A × C · B
得
D = D × E2 · E1
D1 = D × E2 · T
D2 = T × E1 · D
D3 = T × E1 · E2
设
P = D × E2
Q = T × E1
得到最终公式:
u = \(\frac{\bf{P} · \bf{T}}{\bf{P} · \bf{E_1}}\)
v = \(\frac{\bf{Q} · \bf{D}}{\bf{P} · \bf{E_1}}\)
t = \(\frac{\bf{Q} · \bf{E_2}}{\bf{P} · \bf{E_1}}\)
代码如下:
bool IntersectTriangle(const Vector3& orig, const Vector3& dir,
Vector3& v0, Vector3& v1, Vector3& v2,
float* t, float* u, float* v)
{
// E1
Vector3 E1 = v1 - v0;
// E2
Vector3 E2 = v2 - v0;
// P
Vector3 P = dir.Cross(E2);
// determinant - P·E1
// 根据混合积公式的几何意义,det是E1&E2&OP组成的平行四边体的有向体积。
float det = E1.Dot(P);
// 保证det > 0, 响应的修改T。
Vector3 T;
if (det > 0)
{
T = orig - v0;
}
else
{
T = v0 - orig;
det = -det;
}
// 如果determinant接近0,也就是有向体积接近0,就说明射线和E1&E2平面共面。
if (det < 0.0001f)
{
return false;
}
*u = Vector3::Dot(T, P);
if (*u < 0.0f || *u > det)
{
return false;
}
// Q
Vector3 Q = Vector3::Cross(T, E1);
*v = Vector3::Dot(dir, Q);
if (*v < 0.0f || *u + *v > det)
{
return false;
}
*t = Vector3::Dot(E2, Q);
float invD = 1.0f / det;
*t *= invD;
*u *= invD;
*v *= invD;
return true;
}
实际应用可参考:github传送门