游戏按照镜头视角来分,可以分为2D游戏、3D游戏,除此之外还有一类游戏被称为2.5D游戏。这是一个比较有争议的分类,这个分类有着不同的解释。有的人认为这只是厂商的噱头,它本身就是2D游戏(我曾经也这么认为,直到亲自做了一款2.5D游戏);也有的人认为他是介于2D和3D之间的一种游戏类型,通常把斜视角的2D游戏称作2.5D游戏。
历史
2001年,盛大游戏推出了一款大型多人在线角色扮演游戏(MMORPG),风靡大江南北,那就是《热血传奇》。《热血传奇》被誉为中国网游的鼻祖,除了它很多开创性的玩法以外,更重要的在于在那个年代其画面的震撼程度。在那个年代,市面上很少看见画面如此精美的真3D游戏,不少人都被其画面视角蒙蔽,认为这就是一款精美的3D游戏。网络上有这么一句俗话:“游戏之于玩家,就像女人之于男人,必须重于画面”。《热血传奇》这一手以假乱真的伪3D,忽悠得不少懵懂无知的少年为其欲罢不能。
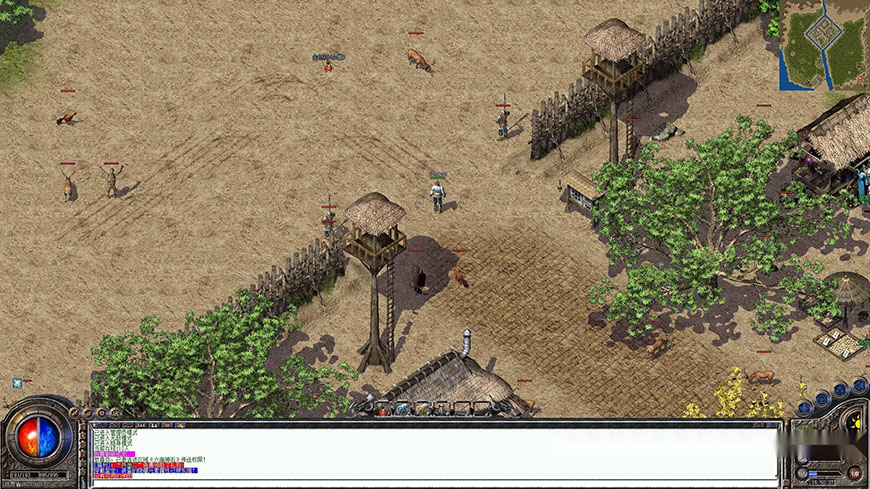
对比起同时代的Pokémon等2D游戏来说,其3D感更强。其中原因,除了绘画的精致外,更重要的是镜头朝向着游戏世界的侧面,而不是那么“耿直”的朝向游戏世界的正面。

除了《热血传奇》,还有一些即时战略游戏(RTS)游戏也尝试了2.5D视角,并取得了成功,比如《红色警戒》、《星际争霸》。
随着游戏渲染技术的发展,大部分游戏都已经抛弃了2.5D的做法,转而做纯3D游戏了,但是现如今也还有一批游戏仍旧以2.5D的方式去渲染游戏。简单的分析可能是基于以下几点因素:
-
游戏成本限制,3D游戏需要复杂于2D游戏的制作流程、人员配置,会提高游戏成本
-
3D模型细节程度和画面渲染效率成反比,为了在高效运行效率的前提下,保留更多的模型细节
比如绝大部分“三消+”游戏,代表就是俄罗斯公司Playrix的《梦幻家园》,可见房间内部的每一个物件的细节都很精美地表现了出来。这些细节要是用3D模型的方式去做将会带来巨大的性能开销。

问题
2.5D游戏仅仅是在2D游戏基础上把视角横向旋转了45度,但是制作难度却高出了不少。
2.5D视角带来的最核心的问题是每个图片和其他图片之间的遮挡关系如何处理,才能更符合人类对3D世界的常识性认知呢,也就是用2D的方式来模拟3D。
2D游戏的做法很简单粗暴。2D游戏世界中每一个物件都会用一个2维坐标来表示其位置,x表示其横向位置,y表示其纵向位置。当一个物件的y值越小,也就是其越靠近画面底部,则渲染顺序越靠后。就像一个画家在Photoshop上作画一样,离相机越近的图层要越后面画,才能盖住离相机远的图层,所以画家要从远到近地画。
但是2.5D却不能用这么简单的规则去解决问题,如下图所示。

P1点的y值大于P2点的y值,如果按照2D游戏的做法,桌子应该是挡住花瓶的,那样就无法模拟3D世界了。
建立坐标系
在构建坐标系之前,我们需要了解真3D游戏是如何渲染出来的。3D游戏的渲染,简单来说可以理解为将三维数据在二维平面上做投影的过程。所以所谓的3D游戏,呈现在玩家面前依然是一个二维的画面,三维空间中的物件移动表现在二维画面上,也就是二维坐标位置的移动而已。
基于此结论,为了尽可能模拟3D视角下物件的移动表现,我们建立一个新的坐标系,这个坐标系是基于视口平面的坐标系,如下图所示。
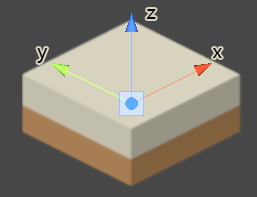
x,y,z三个向量在游戏引擎的3D世界空间中,其实是跟相机视口共面的。我们以这三个向量为基底,构建出一个3D空间坐标系,下文中我们把这个空间坐标系命名为Iso空间。
如图所示,从视觉上我们很容易将图中菱形元素看做一个斜视角下的立方体,如果立方体在Iso空间中位置的x值增大,那么立方体将会向屏幕的右上方移动,视觉上好像立方体向着自己的水平方向移动了一样。因此我们完全可以在一个2D平面上通过斜方向移动图片,来欺骗视觉,造成物件在3D空间中移动的错觉。
视角选择
通常2.5D游戏会被人们称为斜45度视角游戏,但是斜45度真的是观察3D物件最佳的倾斜角度吗?
评估最佳与否,我们姑且确定一个标准,在不影响美观的前提下,尽可能地简化开发难度,节约开发成本。
要做这个评估,我们首先得了解3D物件投影到屏幕上的具体情况。
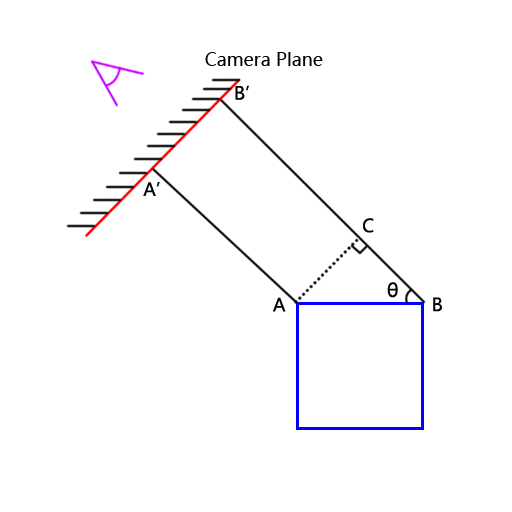
如图所示,如果我们要把3D空间中的一个立方体(图中蓝色部分)显示到相机屏幕(图中红色部分)上,将会经历上图投影变换。
假设现在要把线段AB投影成相机平面上的线段A’B’,我们可以作两条辅助线BB’和AA’,使得BB’平行于AA’,过A点作辅助线AC垂直于BB’,那么求A’B’就转化为求AC。
由三角函数公式可以知道,AC = AB * sin(θ),又因为θ就是相机的俯仰角,即为我们的所求。所以3D线段和投影线段之间的关系为:投影线段 = 3D线段 * sin(俯仰角)。
再回到3D相机视角,如果相机正对着的是一个正方形,那么斜视角下投影到相机屏幕上将会是一个菱形,这个菱形的宽高比随着相机俯仰角度不同而不同。为了模拟表现出这种视角关系的画面,美术人员就需要做一张菱形的图片贴在屏幕上,以拟合正交3D投影。
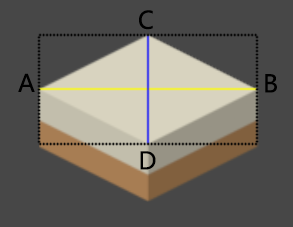
如上图所示,如果美术想表示一个3D世界中的正方形,那么他需要制作一张菱形贴图(虚线框内部分)。由于相机俯仰运动时的旋转轴平行于AB方向,故而AB的长度即为正方形在3D世界中的真实长度。CD长度垂直于俯仰旋转轴,根据上述公式可得CD长度=3D世界中正方形CD长度 * sin(俯仰角)。
为了切图方便,美术会把贴图的长宽像素值都设为整数,因为美术无法切出0.5个像素的图片,那么就要求AB和CD都是整数。如果俯仰角θ也是整数,将会让美术很方便地调整模型制作软件(如Maya、3ds max等)的相机角度,通过3D渲染,将3D模型烘焙成2D图片,以供游戏中直接使用。
遍历三角函数查找表,只有sin(30°)和sin(60°)是有限小数,也就是只有这两个角度有可能让长宽都为整数。通过尝试60°俯视角的相机位置太过于高,不利于美术表现,30°俯视角的相机位置处于美术可接受范围,故而30°俯视角是最佳倾斜角,也就是说图片宽高比为1:2。
通过观察与分析,市面上许多游戏都是斜30°视角游戏,例如《梦幻家园》。这些游戏都通过实践验证了最佳倾斜角理论。因此人们通常说的斜45度视角游戏只是人们通过臆测而给2.5D游戏取得俗名,准确来说我们应该称这类游戏叫做斜30度视角游戏。或者可以采用另一种对斜45度视角游戏的解释,斜45度指的是相机水平方向上(围绕世界空间Y轴)的旋转角度。
空间变换
上文讲到我们为了模拟3D运动,建立了一套坐标系,那么这套坐标系和世界空间坐标系有什么样的联系呢?
通常为了描述两个坐标系之间的关系,我们会求出一个变换矩阵,通过变换矩阵和变换矩阵的逆矩阵,将两个不同坐标系下的对应点位置进行转换。
那么,Iso空间的坐标点是如何转化为世界空间坐标点的呢?下图展示了一个Iso空间下的正方形如何转化为世界空间下的菱形的过程。
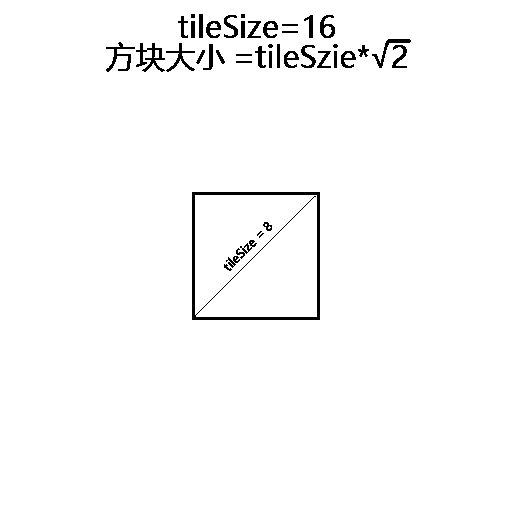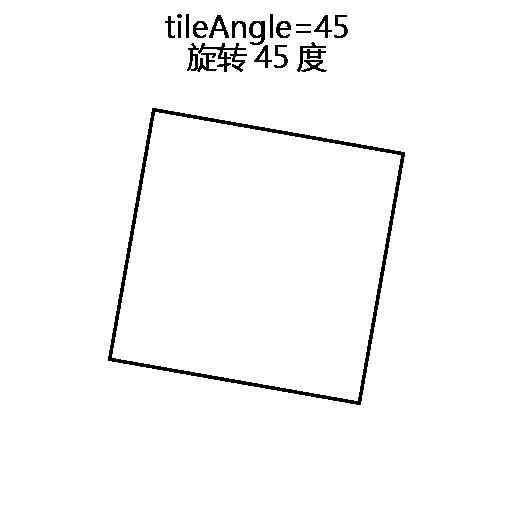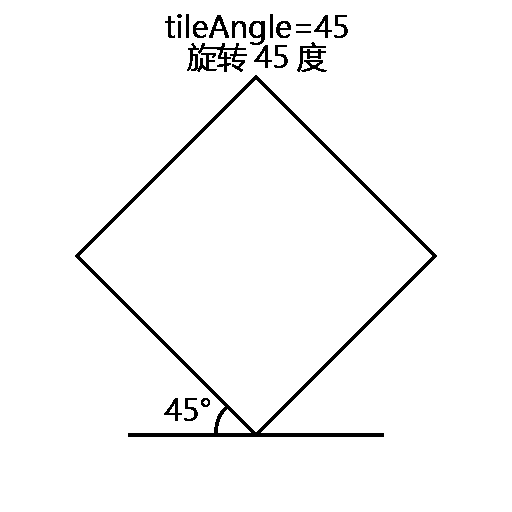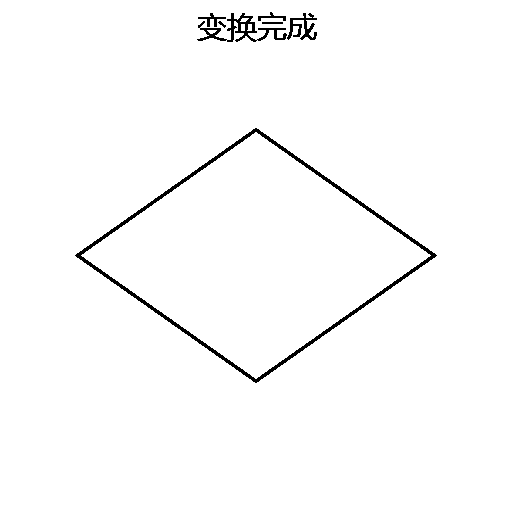
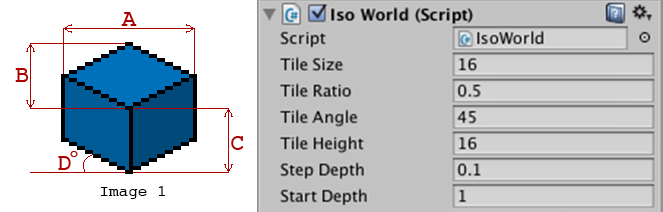
由图可知,为了做这个变换,需要三个关键的参数:tileSize、tileAngle、tileRatio。例如图中所表达的意思就是:正方形大小为16个Unit;相机水平旋转45度(通过围绕世界空间Z轴旋转图片来模拟);相机倾斜30°,也就是上文中所说宽高比为1:2(通过Y方向缩放图片大小来模拟)。我们可以定义一个类IsoWorld来存放这些变换所需的参数,以及提供空间变换的接口。
public class IsoWorld
{
float tileSize { get; set; } // 图中的A值
float tileAngle { get; set; } // 图中的D值(其实不准确是D值,参考变换过程动图)
float tileRatio { get; set; } // 图中的B和A的比值:B除以A
float tileHeight { get; set; } // 图中的C值
// 从Iso空间的三维坐标转换为屏幕上世界空间的二维坐标
// iso - Iso空间的三维坐标
// [return] - 转换后的屏幕上世界空间的二维坐标
Vector2 IsoToScreen(Vector3 iso);
// 从屏幕上世界空间的二维坐标转换为Iso空间的三维坐标
// pos - 屏幕上世界空间的二维坐标
// iso_z - 指定的Iso空间Z值
// [return] - 转换后的Iso空间的三维坐标
Vector3 ScreenToIso(Vector2 pos, float iso_z = 0.0f);
}
其中核心的坐标变换,也就是变换过程的动图效果的实现代码如下所示。
// public static Vector3 vec3OneZ { get { return new Vector3(0.0f, 0.0f, 1.0f); } }
_isoMatrix =
Matrix4x4.Scale(new Vector3(1.0f, tileRatio, 1.0f)) *
Matrix4x4.TRS(
Vector3.zero,
Quaternion.AngleAxis(90.0f - tileAngle, IsoUtils.vec3OneZ),
new Vector3(tileSize * Mathf.Sqrt(2), tileSize * Mathf.Sqrt(2), tileHeight));
因此可以给每一个物件定制一个组件,更直观地控制该物件的Iso坐标。
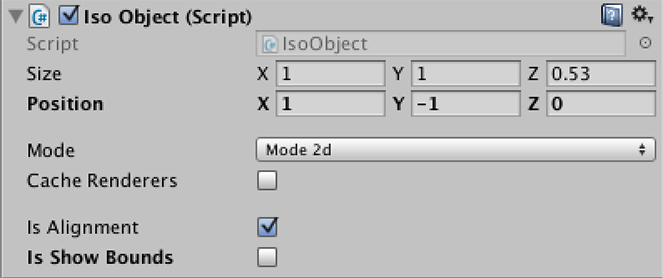
从上图可以看出,我们不再去操作transform.position,取而代之的是通过修改IsoObject.position去调整物件位置。
遮挡排序
上文中已经构建出一套完整的坐标系体系,这套坐标系不仅可以和世界空间相互转换,还能像3D工程一样去思考问题、摆放物件。这点很重要,虽然维度从二维升为了三维,但是这让问题更容易理解,因为可以借用3D工程解决问题的思路去解决2D工程很难处理的一些问题。游戏世界维度的上升反而使得思考问题的难度下降了。
那么回到最开始我们提出的问题上,如何去解决2.5D游戏的遮挡排序问题呢?
3D游戏中,通常是离摄像机越远的物体越先绘制,那么怎么判断一个物件离相机远还是近呢?假设给每一个物件都套上一个AABB盒,那么通过AABB盒去判断离摄像机远近将会是一件非常容易的事。
同理,在Iso空间中,我们给每一个物件生成一个AABB盒,盒子恰好能包裹住物件,如下图(左)所示红色外框就是物件的AABB盒。
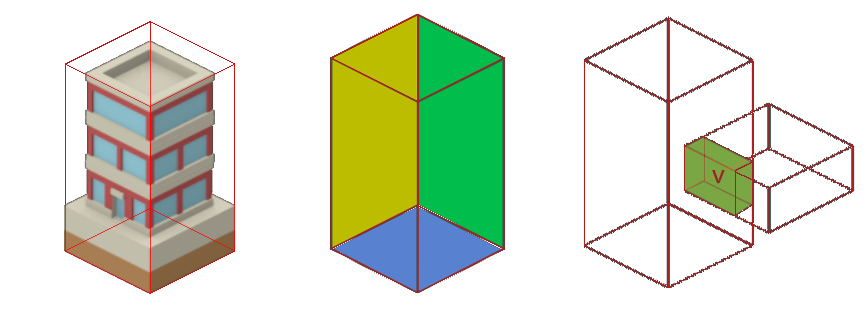
在2.5D世界中根据AABB盒,怎么确定一个物件是先渲染还是后渲染呢?如上图(中)所示。
-
如果B物体的AABB盒在A物体的AABB盒的「黄色面」或者「绿色面」之后,那么A物体遮挡B物体,B物体要先于A物体绘制。
-
如果B物体的AABB盒在A物体的AABB盒的「蓝色面」之下,那么A物体叠加在B物体之上,B物体要先于A物体绘制。
-
如果A物体的AABB盒和B物体的AABB盒相交,如上图(右),那么相交立方体V取最薄的方向,决定使用「黄色面」、「绿色面」还是「蓝色面」来判断位置关系,再返回前两条规则继续计算。
例如如图(右)所示,因为A物体和B物体相交形成的立方体在X轴方向上最薄,所以需要以「绿色面」来判断A和B的位置关系。
核心代码如下。
// 判断AB物体绘制的先后顺序
// a_min - A物体AABB盒的最小坐标值
// a_size - A物体AABB盒的尺寸
// b_min - B物体AABB盒的最小坐标值
// b_size - B物体AABB盒的尺寸
// [return] - 是否B物体要先于A物体绘制
bool IsIsoObjectDepends(Vector3 a_min, Vector3 a_size, Vector3 b_min, Vector3 b_size)
{
a_min = a_min - a_size * 0.5f;
b_min = b_min - b_size * 0.5f;
var a_max = a_min + a_size;
var b_max = b_min + b_size;
var a_yesno = a_max.x > b_min.x && a_max.y > b_min.y && b_max.z > a_min.z;
var b_yesno = b_max.x > a_min.x && b_max.y > a_min.y && a_max.z > b_min.z;
// 如果A和B有相交部分
if (a_yesno && b_yesno)
{
var da_p = new Vector3(a_max.x - b_min.x, a_max.y - b_min.y, b_max.z - a_min.z);
var db_p = new Vector3(b_max.x - a_min.x, b_max.y - a_min.y, a_max.z - b_min.z);
var dp_p = a_size + b_size - IsoUtils.Vec3Abs(da_p - db_p);
// 比较相交部分立方体的X、Y、Z三个方向的厚度,取最薄的部分来作位置关系判断
if (dp_p.x <= dp_p.y && dp_p.x <= dp_p.z)
{
return da_p.x > db_p.x;
}
else if (dp_p.y <= dp_p.x && dp_p.y <= dp_p.z)
{
return da_p.y > db_p.y;
}
else
{
return da_p.z > db_p.z;
}
}
// 如果a_yesno == true && b_yesno == false,则说明B物体要先于A物体绘制
return a_yesno;
}
总结
本文代码主要思想提取自一款名为Isometric 2.5D Toolset的插件。本文主要介绍了一种2.5D游戏的实现的底层方案,以及介绍了其原理,解决了以下问题:
-
3D世界空间和2.5D世界空间的相互转换
-
2.5D世界中的遮挡排序算法
如果有兴趣可以详细研究一下该插件的API及其源代码,除了以上问题,插件还提供了3D&2D混合排序、2.5D物理、鼠标输入处理等功能。如果时间允许,未来2.5D专栏将会细聊一些2.5D工程开发中遇到的问题以及解决方案。