- 立体角
- 辐射能
- 辐射通量
- 光通量(Luminous Flux)
- 光强度(Luminous Intensity,光强)
- 光照度(Illuminance)
- 光亮度(Luminance)
- 光照物理基本物理量总结
- 光照度和光亮度的关系
- 反射系数(Reflection Coefficient)
- 渲染方程(Rendering Equation)
- 总结
- 引用
长期以来CG界都面临着一个问题,如何才能更真实地模拟现实世界的光照?在1986年,吉姆·卡吉雅(Jim Kajiya)的论文[1]提出的渲染方程(Rendering Equation)成为了解决这一问题的开端。2012年的SIGGRAPH大会上,卡吉雅也因此获奖。
渲染方程的物理基础是能量守恒,所以我们先来理解一下一些光照物理上的基础概念。
立体角
在讲述物理概念之前,先明确一个几何概念,立体角。立体角类比平面空间中的平面角,是用来描述三维空间中的角度的数值。
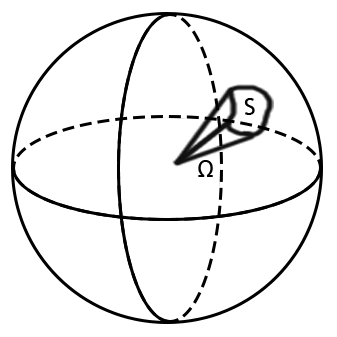
立体角常用字母Ω表示。我们知道,在平面中角度的描述公式为
\[θ = \frac{l}{r}\]也就是角度等于弧长与半径之比。类似的在三维空间中,我们用弧面面积与半径平方来描述三维空间的角度,也就是立体角。设面积为S,半径为r,则
\[Ω = \frac{S}{r^2}\]因为完整球体的表面积为\(4{\pi}r^2\),所以球体的立体角为\(4{\pi}\)。
辐射能
光线本身会以辐射的形势向空间释放能量,这种能量叫做辐射能。辐射能作为一种能量,单位也就是焦耳(J),常用字母Q来表示。光线照射的过程本来就是能量释放的过程,但是光线的强弱并不能以辐射能大小来判断,比如太阳每秒辐射到地球的能量为\(1.75 × 10^{17}\)焦耳,这时人们看到的太阳光很强烈,但是如果这么多能量不是一秒钟以内照射到地球,而是十分钟内照射到地球,那么这种光就会变暗许多。因此物理上通常用功率来描述能量作用的多少。
辐射通量
日常生活中经常会听到某个灯泡是多少瓦这种说法,通过说法可以描述一个光源的明亮程度,这种说法其实就是在描述一个光源的辐射通量。辐射通量也叫辐射功率,指单位时间内,光源发射的总辐射能量,单位瓦特(W),常用字母Φ表示。由于光源辐射能量并不会是平均的,所以设微分能量dQ在微分时间dt内释放的能量为Φ,则
\[Φ = \frac{dQ}{dt}\]光通量(Luminous Flux)
然而我们会发现一个问题,通过辐射通量来描述一个光源的明亮程度并不那么合理。例如同时买了一个40W的白炽灯和一个40W的日光色荧光灯,我们会观察到荧光灯比白炽灯更明亮,但又并非两盏灯功率不一样。出现这种现象的原因有两点。第一,人的眼睛之所以能看到七种颜色的光,是因为这些波段的光线都比较容易在水里传播,地球上的生命源于海洋,只需要看到这些光线即可生存,所以人类只看得到这个波段的光,超出可见光波段的光将会以红外线、紫外线灯看不见的能量形式传播;第二,人眼对不同波段的光视见率不同,所以对于可见光来说,颜色不同人类也会觉得明亮程度不同。针对第二点理论,通常用光通量来描述人眼感受到的光的辐射功率。
光通量作为一种功率也是常用Φ来表示,单位光瓦、流明(lm)。设波长为λ,该波长光线对应的光通量为Φ(λ),那么
\[Φ(λ) = \frac{dΦ}{dλ}\]通常一只40W的白炽灯光通量约为460lm,一只40W的日光色荧光灯光通量约为2100lm。
光强度(Luminous Intensity,光强)
光通量只能描述光源做功的效率,然而光线从光源发射出来并不是均匀的,在中国有一个粗略的单位来描述光线,也就是通常所说的“一缕光线”。那么如何来描述“一缕光线”的强弱呢?这里引入光强度这个物理量来描述光线的强弱。
光强度指的是光源给定方向单位立体角内的光通量,常用I来表示,单位坎德拉(cd)。
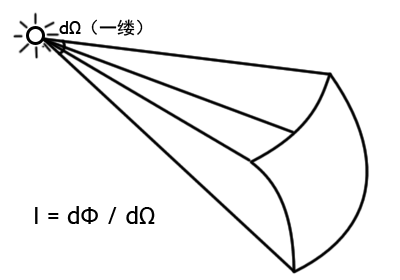
由光强度定义可得
\[I = \frac{dΦ}{dΩ}\]故 1cd = 1lm/sr。
光照度(Illuminance)
现实生活中,人眼要能感觉到光线的存在由两种方式。一种方式就是直接盯着光源看,会看到一片明亮;另一种方式,光线需要照射到某个平面,通过平面把光线反射到人眼睛里,人眼才能感受到明亮。由第二种感知光线的方式推断,人眼感觉到光线的多少还与光线照射的面积大小有关,于是我们使用光照度来描述。
光照度指单位面积上接受的光通量,常用E来表示,单位勒克斯(lux、lx)。
\[E = \frac{dΦ}{dS}\]故\(1lx = 1lm/m^2\)。
如果光通量Φ均匀的分布(各项同性)在被照面S上,那么\(E = \frac{Φ}{S}\)。
由于球体表面积\(S = 4πr^2\),因此对于各向同性的光源来说可得
\[E = \frac{Φ}{4πr^2}\]因此可知光照度是会随着传播距离衰减的。
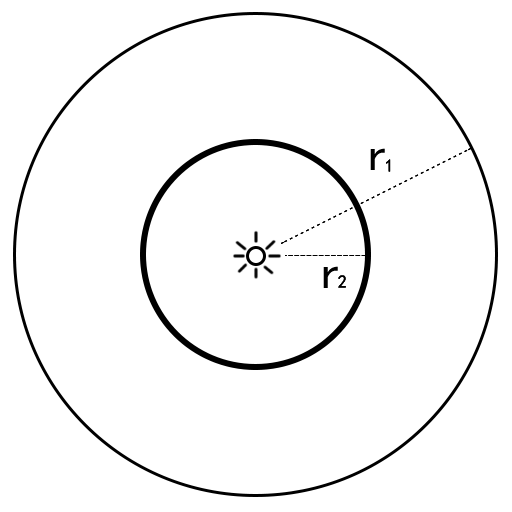
设球面1的半径为\(r_1\),球面2的半径为\(r_2\),那么根据上面公式可得
\[\frac{E2}{E1} = \frac{r_1^2}{r_2^2}\]这也就解释了为何火星上要比地球上冷,因为火星离太阳更远,所以火星表面的光照度更低,导致火星单位面积接收到的辐射通量很低,也就更冷,光线也更暗。
光亮度(Luminance)
接下来,思考一个问题,为何傍晚的地面会比正午的地面昏暗?
这里我们来做一个形象的分析,因为光具有波粒二象性,因此可以把光源理解成发射光子颗粒的发射器。假设某一平行光光源有一定的面积,如果用和光源面积相同的平面,垂直于光传播方向来接收光子,那么平面将会接收所有光子。
如下图所示为这一平行光光柱的侧截面,每一个箭头可以理解为一个光子。
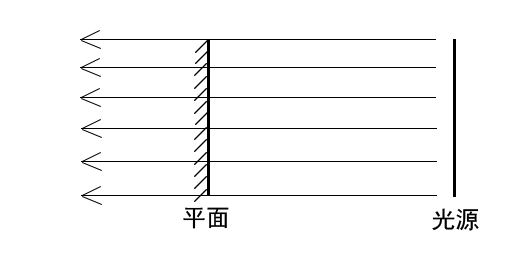
可知光源发出的六个光子都被平面接收到了。如果将平面倾斜一定角度,如下图所示。
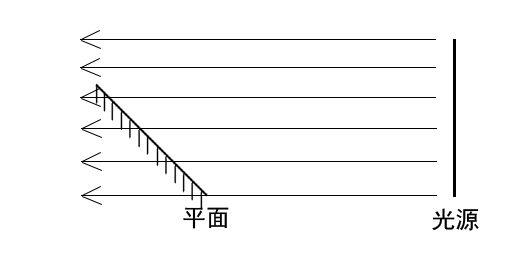
可知光源发出的六个光子只有四个被接收到了。
因此,当接收平面和光传播方向不垂直的时候,平面接收到的光通量也就变少了,那么平面也就会变得更暗。这也就解释了为何傍晚的地面会比正午的地面昏暗。
那么倾斜角度到底和接收到的光通量存在什么关系呢?
假设光在空间中的传播是连续且均匀的,那么接收到光的多少,与接收平面在垂直于光传播方向平面的投影的面积有关。如下图所示。
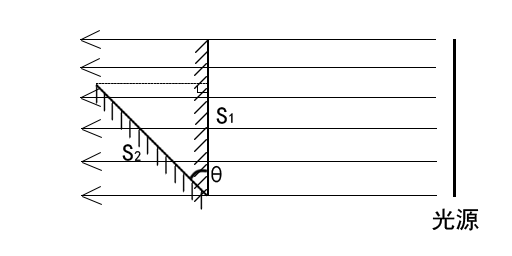
因为\(S_2\)和\(S_1\)面积相同,其面积设为S,那么平面\(S_2\)在平面\(S_1\)上的投影面积等于S×cos(θ)。设垂直于光传播方向的平面\(S_1\)的光照度为\(E_1\),设\(S_2\)的光照度为\(E_2\),那么可得
\[E_2 = \frac{Φ}{S_2} = \frac{Φ}{S_1}·cos(θ) = E_1·cos(θ)\]这也解释了兰伯特定律
因此这里引入了一个物理量来描述平面的明亮程度,我们称之为光亮度。
光亮度,指在某方向上单位投影面积的面光源沿该方向的发光强度,常用L来表示,单位尼特(nit,该单位已过时,更多使用\(cd/m^2\))。
设微表面面积为dS,光的方向和微表面方向夹角为θ,那么微表面垂直于光传播方向的投影\(dS' = dS · cosθ\),则光源在该方向上的亮度为
\[L = \frac{dI}{dS'} = \frac{dI}{dS · cosθ}\]又由于\(dI = \frac{dΦ}{dΩ}\),则光亮度又可以写作
\(L = \frac{dΦ}{dΩ·dS·cosθ}\)。
光照物理基本物理量总结
以上都是基于人眼主观感受得出来的物理量,另外还有一种物理量是基于真实能量的,即辐射通量、辐射强度、辐射照度、辐射亮度。因为渲染更多是基于人眼的感受来实施的,这里就不再详细描述辐射相关物理量。
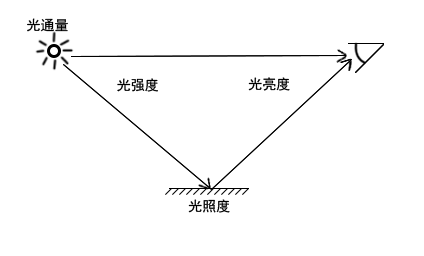
由上图可知,光通量是描述光源自身亮度的,光强度是描述光线强度的,光照度是描述平面接收到的光能的多少,光亮度是描述眼睛感受到的光能的多少。
| 物理量 | 定义 | 符号 | 单位 |
|---|---|---|---|
| 辐射能 | 物体以电磁波或粒子的形式射或输送能量的过程 | Q | 焦耳(J) |
| 辐射通量 | 单位时间内,光源发射的总辐射能量 | Φ | 瓦特(W) |
| 光通量 | 人眼能感觉到的辐射功率 | Φ | 光瓦、流明(lm) |
| 光强度 | 光源给定方向单位立体角内的光通量 | I | 坎德拉(cd) |
| 光照度 | 单位面积上接受的光通量 | E | 勒克斯(lux、lx) |
| 光亮度 | 在某方向上单位投影面积的面光源沿该方向的发光强度 | L | 尼特(nit,该单位已过时,更多使用\(cd/m^2\)) |
光照度和光亮度的关系
通常我们表示立体角方向习惯用ω,而表示立体角时候才用Ω,结合上文光亮度的表示方法可得
\[L = \frac{dΦ}{dω·dS·cosθ}\]同时,光照度可以如下表示
\[E = \frac{dΦ}{dS}\]因此设p点接受到ω方向的光线后的光亮度为L(p, ω),p点的光照度为E(p),则
\[L(p, ω) = \frac{dE(p)}{dω·cosθ}\]得
\[dE(p) = L(p, ω)cosθdω\]即
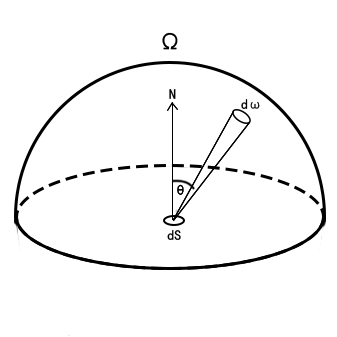
\[E(p) = \int_{Ω}{L(p, ω)cosθdω}\]这里的Ω表示半球的立体角度,也就是在半球上,对来自不同方向的光线做光亮度积分,也可以说是对该点所有微平面接收到的光亮度做积分。半球下的光被物体本身遮挡,对照明没有贡献,所以不考虑半球以下光线。通过对半球光亮度积分,最终得到这一点上的光照度,这就是光照度和光亮度之间的关系。
反射系数(Reflection Coefficient)
上文介绍了描述光照的一些物理量,我们发现除了这些物理量,物体表面的亮度还与物体材质有关,比如白纸就是要比墨亮一些。这是因为不同物体有着不同的反射系数。
从光源照射到平面上的光叫做入射光(incident light),照在平面上的光的总量可以用光照度来度量;从平面反射到眼球中的光叫做发射光(reflection light),反射出光的总量可以用光亮度来度量。反射系数指的就是反射光的总量与入射光的总量之比值。
例如,一般白纸大约吸收入射光量的20%,反射入射光量的80%,但是黑纸只反射入射光量的3%。
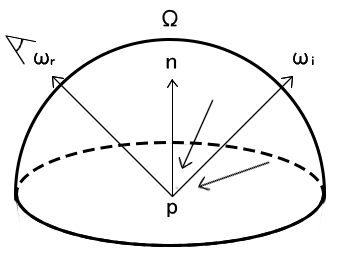
设反射系数为\(f_r\),入射光方向为\(ω_i\),反射光方向为\(ω_r\)。从微观上讲,平面上每一个点都是由很多微表面组成,那么微表面上的反射光亮度为\(dL_r(ω_r)\),微表面上入射光照度为\(dE_i(ω_i)\),反射系数我们可以如下表示
\[f_r = \frac{dL_r(ω_r)}{dE_i(ω_i)}\]根据光照度和光亮度的关系可得
\[f_r = \frac{dL_r(ω_r)}{L_i(ω_i)cosθ_idω_i}\]即
\[L_r(p, ω_r) = \int_{Ω}{f_rL_i(p, ω_i)cosθ_idω_i}\]渲染方程(Rendering Equation)
设某一点的光亮度为\(L(p, ω_r)\),通常由于物体本身靠反射光线来让人眼感受到光照,所以设反射光亮度为\(L_r(p, ω_r)\)。但是这里考虑到某个物体有可能本身是个光源,可能带有自发光项,所以设自发光项为\(L_e(p, ω_r)\)。那么渲染方程可分为反射和自发光两个部分。
\[L(p, ω_r) = L_e(p, ω_r) + L_r(p, ω_r)\]将反射系数的反射光亮度公式带入上式可得
\[L(p, ω_r) = L_e(p, ω_r) + \int_{Ω}{f_rL_i(p, ω_i)cosθ_idω_i}\]其中cosθ可换成\(ω_i·n\),即
\[L(p, ω_r) = L_e(p, ω_r) + \int_{Ω}{f_rL_i(p, ω_i)(ω_i·n)dω_i}\]这也就是最终的渲染方程。
其中,
\(L(p, ω_r)\)是在特定位置p及角度\(ω_r\)的出射光亮度。
\(L_e(p, ω_r)\)是在同一位置及方向,物体自身发出的光亮度。
\(\int_{Ω}...dω_i\)是入射方向半球的无穷小累加和。
\(f_r\)是在该点从入射方向到出射方向光的反比例。
\(L_i(p, ω_i)\)是该点的入射光在\(ω_i\)方向的光强度。
\(ω_i·n\)是入射角带来的入射光衰减。
总结
渲染方程是渲染领域中的一个核心理论概念,它是基于物理渲染的理论基础,基于物理的渲染过程也就是解开渲染方程的过程。由于计算机不能像人类一样求解微积分方程,所以只能通过近似模拟的方式来得到最终结果,通常使用蒙特卡洛积分方法。接下来会对蒙特卡洛积分求解渲染方程做详细描述,以最大程度模拟真实光照,渲染出接近现实的图像。
引用
[1] Kajiya, James T. (1986), “The rendering equation”, Siggraph 1986: 143–150, doi:10.1145/15922.15902, ISBN 978-0-89791-196-2