基于导航的寻路系统（二）：寻路

导航网格结构
泛型A*求解器
实现寻路
总结

上文介绍了基于导航的寻路系统，本文将详细介绍如何实现在导航网格上实现一套寻路系统，使得地图上两点之间能够找到一条最短路径，以供上层的游戏逻辑使用。

导航网格结构

导航网格模型，类似于图形渲染上所说的网格模型，同样是由某种“图元”组成。渲染上所说的图元通常指的是三角形，而导航网格模型的“图元”则是凸多边形，比如Recast Navigation的网格图元用的就是凸多边形。由于本套导航网格系统的数据来源并非如Recast Navigation一样是自动生成的，而是需要美术人员建模而生成，即FBX文件，所以本导航网格系统的“图元”以FBX通常标准为准，使用三角形作为寻路图元。

以上导航网格模型的结构，使用代码实现如下图所示。

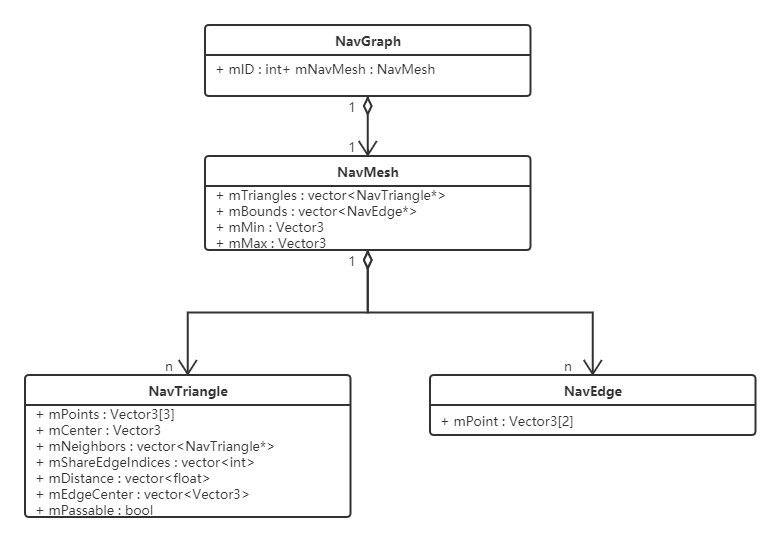
如上图所示，NavMesh也就是上文提到的导航网格模型抽象出来的类，由UML图可以知道，一个NavMesh里包含了多个NavTriangle，而NavTriangle类就对应上文提到的三角形。由上图可知，NavTriangle由以下成员组成：

mPoints：这是由三个Vector3组成的数组，分别代表三角形的三个顶点。
mCenter：这个是三角形的中心点，由三角形的三个顶点之和除以3求得。
mNeighbors：这个列表里包含了0到3个其他三角形的指针，用来访问该三角形相邻的所有三角形。
mShareEdgeIndices：这个int数组存储了共享边的序号，至于什么是共享边的序号，后续会详细介绍。
mDistance：这个列表里包含的数值个数和mNeighbors的个数相同，即该三角形的中心点分别到相邻三角形中心点的距离。
mEdgeCenter：这个列表里包含的数值个数和mNeighbors的个数相同，指的是和相邻三角形邻接边的中点，至于这个中点有什么用，后续会详细介绍。
mPassable：这个变量标明该三角形是否可以通行，后续会详细介绍。

图中的NavMesh类有一个叫做mBounds的列表，该列表里存放了导航网格模型的所有边缘数据，后续会详细介绍，这里先忽略。

图中的NavMesh有两个Vector3变量，分别是mMin和mMax，分别表示导航网格模型的AABB盒最大顶点位置和最小顶点位置。

泛型A*求解器

寻路模块要求准备一个A*求解器，用来承载A*算法。MicroPather是一个用独立于平台的语言C++编写的路径查找器和A*求解器，可以很容易地集成到现有的代码中。MicroPather专注于成为电子游戏的寻路引擎，并且是一个泛型的A*的求解器。MicroPather由于其泛型设计，所以不局限于某一种形式的寻路节点，是一个通用性很强的寻路求解器。

MicroPather集成到项目里非常简单，简单描述就是三个步骤：

将MicroPather的头文件包含（include）进项目
实现Graph接口
调用Solver函数

详细使用说明以及工程地址为：MicroPahter。

现在，介绍一下Graph接口里的两个核心接口方法。

virtual float LeastCostEstimate( void* stateStart, void* stateEnd ) = 0;

该方法用于计算两个点之间的“最小路径长度”，该方法通常在计算“H值”时候被调用。

virtual void AdjacentCost( void* state, MP_VECTOR< micropather::StateCost > *adjacent ) = 0;

该方法用于计算一个节点和它相邻节点的“路径长度”，该方法通常在计算“G值”时候被调用。

以下是求解一条从startState节点到endState节点最短路径的示例。

MicroPather* pather = new MicroPather( myGraph );	// Although you really should set the default params for your game.

micropather::MPVector< void* > path;
float totalCost = 0;
int result = pather->Solve( startState, endState, &path, &totalCost );

示例代码里面的path变量即为最终求解得到的路径。由该示例代码可以看到，这条“路径”只是一个抽象概念，MicroPather可以用于更多抽象的情景。

实现寻路

由前面的UML图可以看到，一个NavGraph里包含了一个NavMesh，那么NavGraph是用来干什么的呢？从代码实现上看，NavGraph实现了Graph接口，所以这个类封装了整套寻路逻辑，且包含了一个NavMesh作为算法数据来源。

class NavGraph : public micropather::Graph
{
	...
};

求解“H值”

float NavGraph::LeastCostEstimate(void* stateStart, void* stateEnd)
{
	if (!stateStart || !stateEnd)
		return MAX_COST;

	NavTriangle* triStart = (NavTriangle*)stateStart;
	NavTriangle* triEnd = (NavTriangle*)stateEnd;
	if (!triStart->mPassable || !triEnd->mPassable)
		return MAX_COST;

	float cost = (triStart->mCenter - triEnd->mCenter).Length();

	return cost;
}

从求解“H值”的代码可以看出两个三角形的距离的求解，用的是两个三角形的中点的距离来计算。另外，如果该三角形不可通过，也就是mPassable为false，则返回其“H值”为MAX，也该三角形就是不能参与路径计算，这部分将会在后续详细描述。

求解 “G值”

void NavGraph::AdjacentCost(void* state, std::vector<micropather::StateCost> *adjacent)
{
	if (!state) return;
	NavTriangle* tri = (NavTriangle*)state;
	for (unsigned int i = 0; i < tri->mNeighbors.size(); ++i)
	{
		NavTriangle* neighbor = tri->mNeighbors[i];

		micropather::StateCost cost;
		cost.cost = tri->mDistance[i];
		cost.state = (void*)neighbor;

		if (!neighbor->mPassable)
			cost.cost = MAX_COST;

		adjacent->push_back(cost);
	}
}

从求解“G值”的代码可以看出，相邻的三角形存放在了每个三角形自己的mNeighbors列表里。其中，三角形的mDistance列表里保存了到所有相邻三角形的距离，计算方式也是通过计算两个三角形中心点距离求得，该列表的所有距离值在创建三角形的时候已经预先计算好并加入列表，避免每次求路径都要反复计算。adjacent列表里保存了当前三角形所有的相邻三角形以及对应的“G值”。

基于三角形的寻路演示

根据以上介绍，制作了一个工具，用来模拟寻路的过程。

先导入FBX到工具，生成导航网格模型，如下图所示。

然后按照工具指示，先后点击两个三角形，第一次点击的三角形为开始三角形，第二次点击的三角形为结束三角形。第二次点击完成，工具会自动生成一条寻路路径，如下图所示。

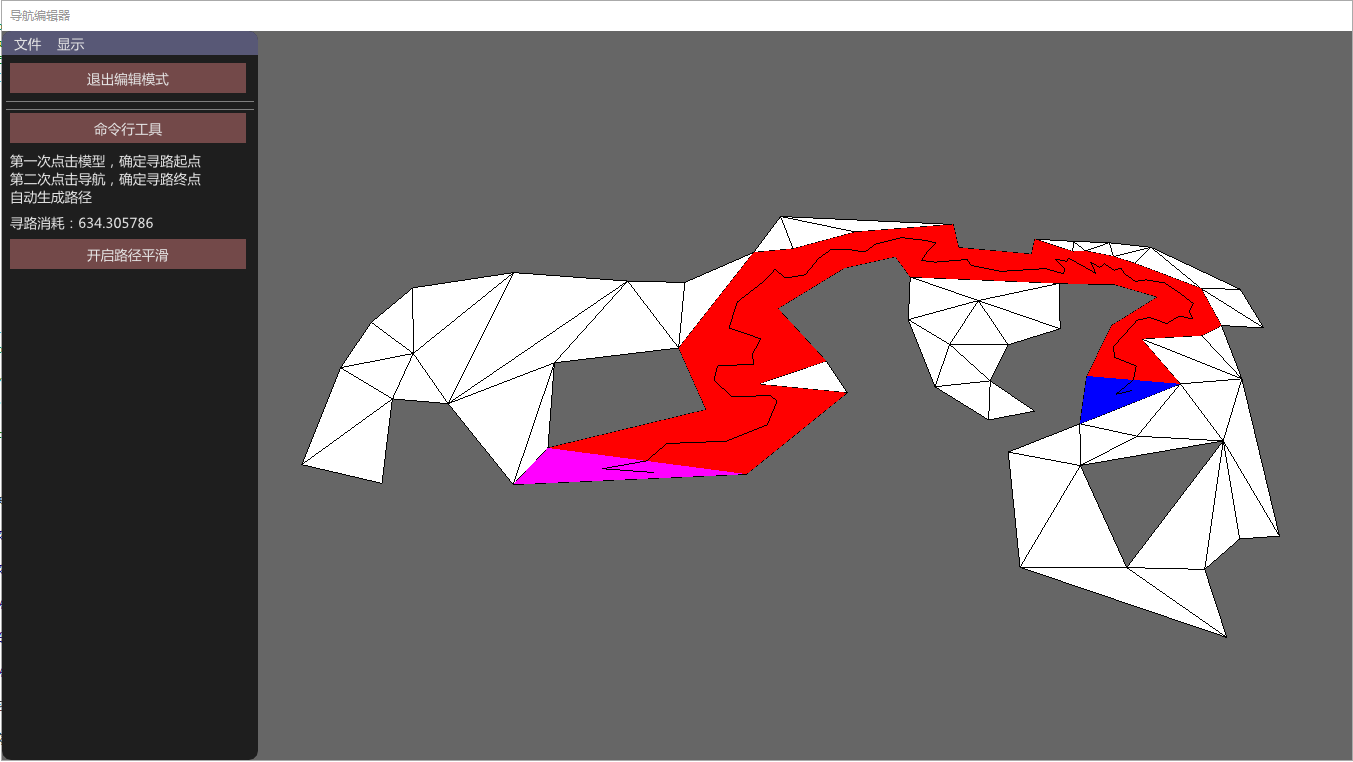
如上图所示，粉红色三角形就是开始三角形，蓝色三角形就是结束三角形，那些红色的三角形就是寻路路径经过的所有三角形。

求解点到点的路径

至此，一个三角形到另外一个三角形的路径已经可以通过求解得到，但是真实游戏中需要的路径是点的集合，而不是三角形的集合。

因此，需要封装一个求解函数以获得点集合的路径。

bool NavGraph::Solve(const Vector3& start, const Vector3& end, std::vector<Vector3>* path, float* cost, bool smoothPath) const
{
	NavTriangle* triStart = GetTriangleByPoint(start);
	NavTriangle* triEnd = GetTriangleByPoint(end);
	std::vector<NavTriangle*> triPath;
	bool rst = Solve(triStart, triEnd, &triPath, cost);
	if (rst)
	{
		path->push_back(start);
		unsigned int nodeCount = (unsigned int)triPath.size();
		for (unsigned int i = 0; i < nodeCount; ++i)
		{
			NavTriangle* tri = triPath[i];
			path->push_back(tri->mCenter);

			if (i < (nodeCount - 1))
			{
				NavTriangle* triNext = triPath[i + 1];
				for (unsigned int j = 0; j < tri->mNeighbors.size(); ++j)
				{
					if (tri->mNeighbors[j] != triNext)
						continue;
					path->push_back(tri->mEdgeCenter[j]);
					break;
				}
			}
		}
		path->push_back(end);
		
		// 路径平滑过程
		...
	}
	return rst;
}

由代码可知求解过程如下：

根据开始点和结束点分别求出开始三角形和结束三角形（GetTriangleByPoint后续会详细介绍）。
根据开始三角形和结束三角形求出三角形集合的路径。
将开始点加入点集合的路径，作为第一个路径点。
将经过的三角形，以及与下一个三角形邻接的边上的中点，都加入点集合的路径。
将结束点加入点集合的路径，作为最后一个路径点。

以上过程求解出来的点集合的路径即为最终寻路路径。

最终寻路效果如下图所示。

总结

本文介绍并实现了一种基于导航的寻路方案。由最终寻路效果图可以看到，该方案实现了一套可行的寻路方案，该方案求解出一条基于位置点的寻路路径以供上层游戏逻辑使用。同时从最终寻路效果图还可以看到，寻路路径弯折太多，这样的寻路路径如果应用到上层游戏逻辑，寻路角色走路的时候将会频繁的转弯，看起来很不自然。为了解决这个问题，将实现一种寻路路径平滑算法，后续文章将会详细介绍。